
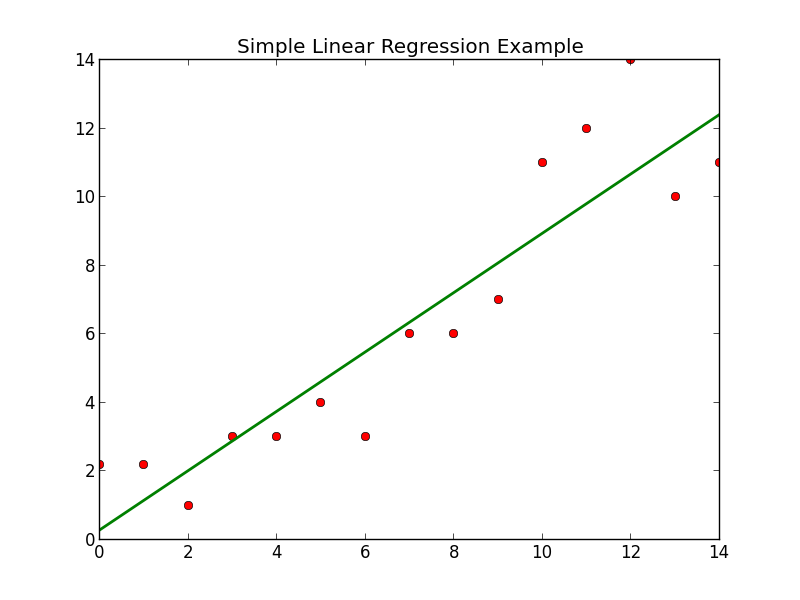

The interpretation of the intercept (value=4.267) is that if there were states with poverty rate = 0, the predicted average for the 15 to 17 year old birth rate would be 4.267 for those states.
The interpretation of the slope (value = 1.373) is that the 15 to 17 year old birth rate increases 1.373 units, on average, for each one unit (one percent) increase in the poverty rate.In statistical notation, the equation could be written \(\hat = 4.267 + 1.373x \). The equation should really state that it is for the “average” birth rate (or “predicted” birth rate would be okay too) because a regression equation describes the average value of y as a function of one or more x-variables. The equation of the fitted regression line is given near the top of the plot. The following plot shows a regression line superimposed on the data. As the poverty level increases, the birth rate for 15 to 17 year old females tends to increase as well. The plot of the data below (birth rate on the vertical) shows a generally linear relationship, on average, with a positive slope. (Data source: Mind On Statistics, 3rd edition, Utts and Heckard). The variables are y = year 2002 birth rate per 1000 females 15 to 17 years old and x = poverty rate, which is the percent of the state’s population living in households with incomes below the federally defined poverty level. This dataset of size n = 51 are for the 50 states and the District of Columbia in the United States ( poverty.txt). Example 1: Teen Birth Rate and Poverty Level Data


 0 kommentar(er)
0 kommentar(er)
